Backpropagation
应用链式法则计算梯度的一种方式
在神经网络中,将训练数据看成是固定的,而权重则是我们可以控制的变量(\(\mathbf{W,b}\))
\(\triangledown f(\mathbf{x})\)是偏导数的向量
过程¶
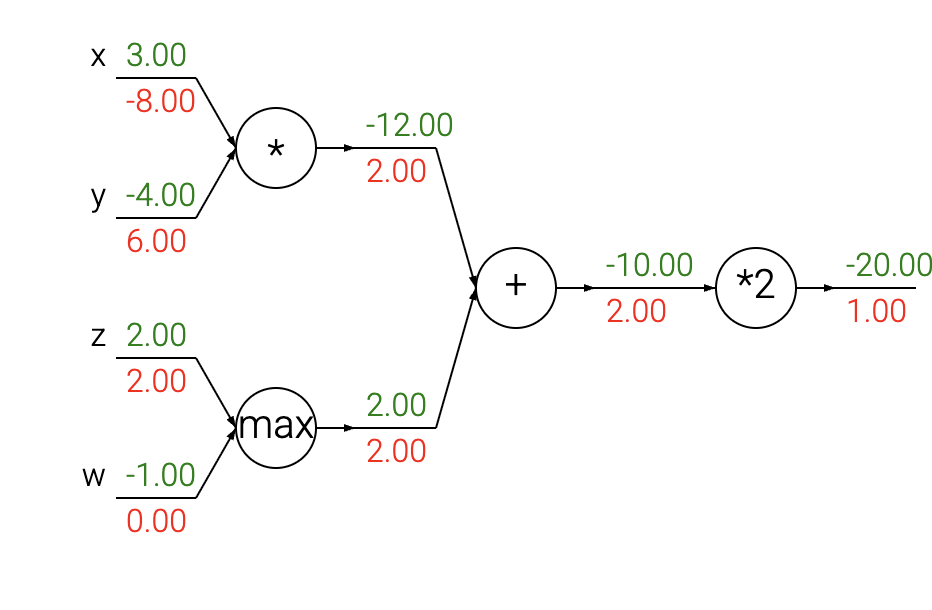
以这张图片为例,反向传播的过程是
- 首先构造计算图,将复杂的函数分解为简单的、可求导的模块,前向传递计算出\(f\)的值
- 从后向前,利用链式法则逐步计算梯度。对于有多个路径影响输出的变量,其总梯度是所有路径梯度的总和
Patterns in backward flow¶
加法门(add gate) 总是接收其输出端的梯度,并将其等同地分配给所有的输入端,无论它们在前向传播(forward pass)时的值是多少。这源于一个事实:加法操作的局部梯度(local gradient)就是+1.0,所以所有输入端的梯度将与输出端的梯度完全相等,因为它们都会乘以1.0(并保持不变)。在上面的电路示例中,请注意 + 门将2.00的梯度路由(routed)给了它的两个输入,数值均等且未经改变。
最大值门(max gate) 路由梯度的方式则不同。与加法门将梯度不变地分配给所有输入不同,最大值门将梯度(同样不变地)精确地分配给它的一个输入——即在前向传播期间值最大的那个输入。这是因为对于最大值门来说,其局部梯度对于值最大的输入是1.0,而对于所有其他输入则是0.0。在上面的电路示例中,最大值操作将2.00的梯度路由给了变量 z(因为它的值比 w 更大),而 w 上的梯度则保持为零。
乘法门(multiply gate) 的解释要稍微复杂一些。它的局部梯度是输入值(但进行了交换),然后根据链式法则,这个局部梯度会与其输出端的梯度相乘。在上面的示例中,x 上的梯度是-8.00,这个值是由-4.00 x 2.00计算得来的。
一些不直观的效果及其后果。请注意,如果乘法门的一个输入非常小,而另一个输入非常大,那么乘法门会做一些稍微不直观的事情:它会将一个巨大的梯度分配给那个小的输入,而将一个微小的梯度分配给那个大的输入。注意,在线性分类器中,权重和数据点积(WTxi)就是一种乘法操作,这意味着数据的尺度(scale)会对权重的梯度产生影响。举个例子,如果你在预处理阶段将所有输入数据样本 xi 都乘以1000,那么权重的梯度将会增大1000倍,你就需要将学习率(learning rate)降低1000倍来补偿。这就是为什么预处理如此重要,并且它会以一些微妙的方式产生影响。对梯度如何流动有一个直观的理解可以帮助你调试其中一些情况。