Linear Classifiers¶

Parametric Approach(参数化方法)¶

$f(x,\mathbf{W}) = \mathbf{W}x + b$

输入向量$x$是图像展开的长向量，$\mathbf{W}$是权重，最后输出的是对于各个类别的得分向量，向量长度等于类别数量

线性分类器对每一种类别都有一个“模版”，图像结果每个模版从而生成分数

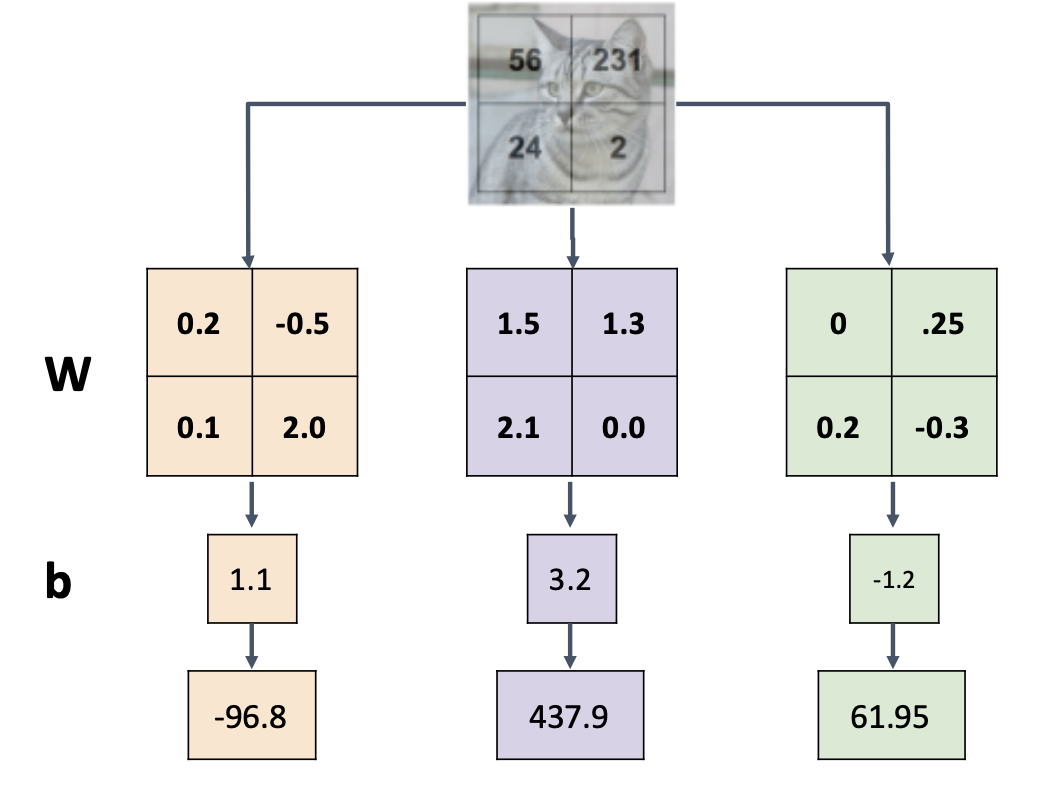
这种方法非常依赖图像中的上下文线索，比如背景的颜色

线性分类器对每一种类别只能学习一个模版，对于同一种类别有多种模式的数据时难以胜任

Geometric Viewpoint: Hyperplanes carving up high-dimensional space

Warning

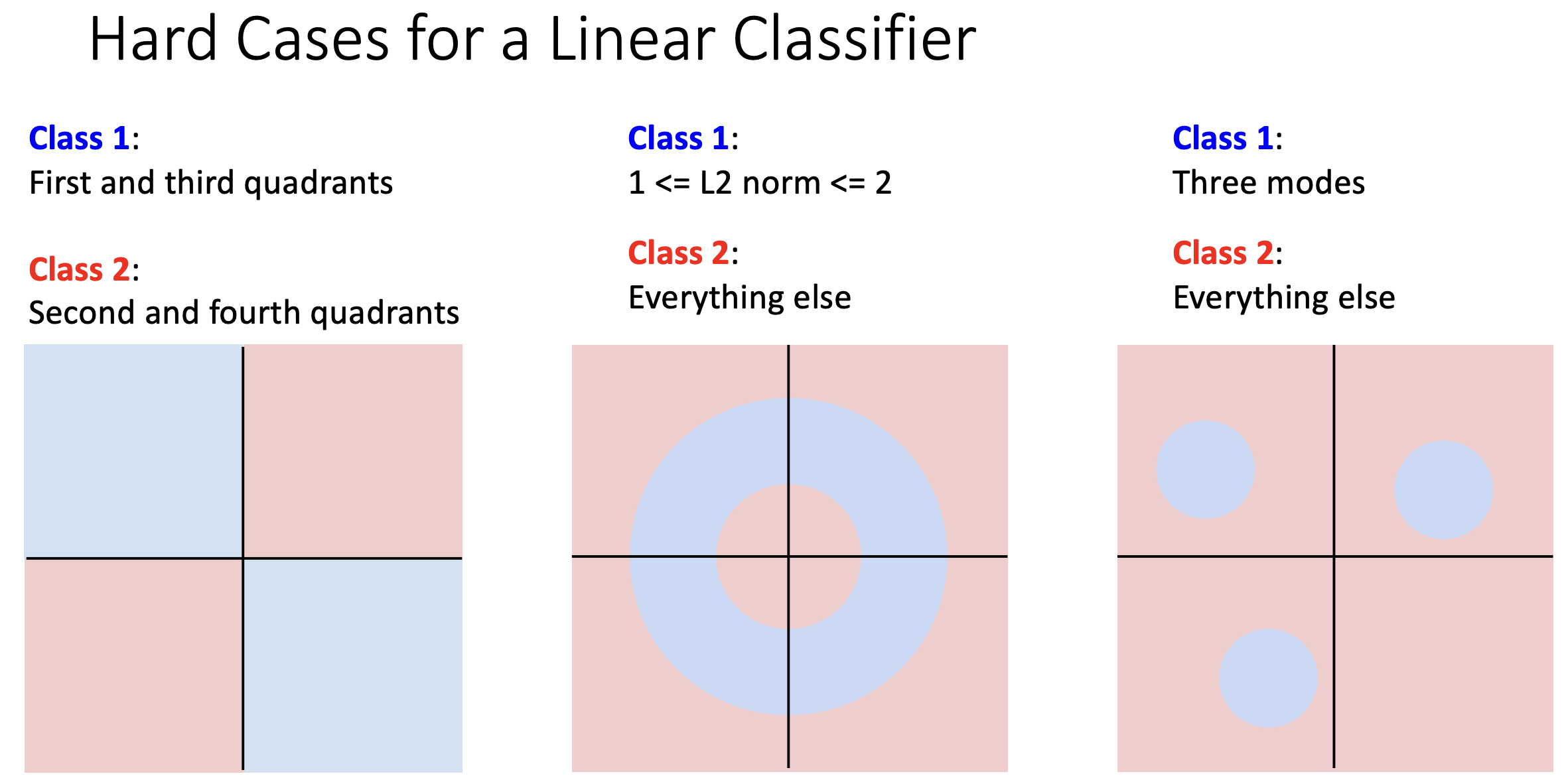
Perceptron 不能实现异或

Define a Linear score function¶

如何选择一个好的权重？ - 使用损失函数来量化权重的质量 - 找到一个使损失函数值最小的权重（optimization）

multi-class SVM Loss:

$$ L_i = \sum_{j\neq y_i} \max(0,s_j-s_{y_i}+1) $$ - 也就是说，对于某一个样本，它实际类别对应的得分如果远大于（我们需要一个边界，就是上图中的+1）某个其他类别的得分，那么该“其他类别”对损失函数的贡献即为0；反之，如果并没有远大于其他某个类别的得分，则需要将这个偏差作为对损失函数的贡献。

正则化¶

防止模型过拟合

L1 范数：$R(W) = \sum_k \sum_l W^2_{k,l}$
L2 范数：$R(W) = \sum_k \sum_l |W_{k,l}|$
Elastic Net： L1+L2

正则化的目的：

在“最小化训练误差”之外，表达对不同模型的偏好。
避免过拟合：偏好泛化能力更好的简单模型。
通过增加曲率来改善优化。

偏好简单的模型

Cross-Entropy Loss¶

Softmax Classifier¶

softmax将得分归一化为概率分布
scores = 未归一化的
$P(Y = k|X = x_i) = \frac{e^{s_k}}{\sum_j e^{s_j}}, where ~s = f(x_i;W)$
$L_i = -log(P(Y = y_i | X = x_i))$

交叉熵损失函数¶

Kullback-Leibler divergence(KL散度):$D_{KL}(P||Q) = \sum_y P(y)log(\frac{P(y)}{Q(y)})$
- 衡量两个概率分布的差异
Cross Entropy: $H(P,Q) = H(p) +D_{KL}(P||Q)$,交叉熵等于信息熵加上KL散度

Cross-Entropy vs. SVM Loss¶

交叉熵 $loss > 0$,SVM loss = 0
在实际使用中，SVM 在保证真实标签对应的得分高于其他得分一定量后就接受了，即存在一个明确的突变标准；而对于 Softmax 来说，它会在这个过程中不断将正确标签对应的概率向1逼近，不断优化自己。