Recurrent Neural Networks
1 Recurrent Neural Networks¶
RNNs 有内部隐藏状态
假设输出是vector \(\mathbf{x}\), $$ h_t = f_W(h_{t-1},x_t) $$ - \(h_t\),new state - \(f_W\), some function with parameters W - \(x_t\), input vector at some time step
2 Venilla RNN¶
\(\(h_t = tanh(W_{hh}h_{t-1}+W_{xh}x_t)\)\)
\(\(y_t = w_{hy}h_t\)\)

Sequence to Sequence: Many to one + One to many

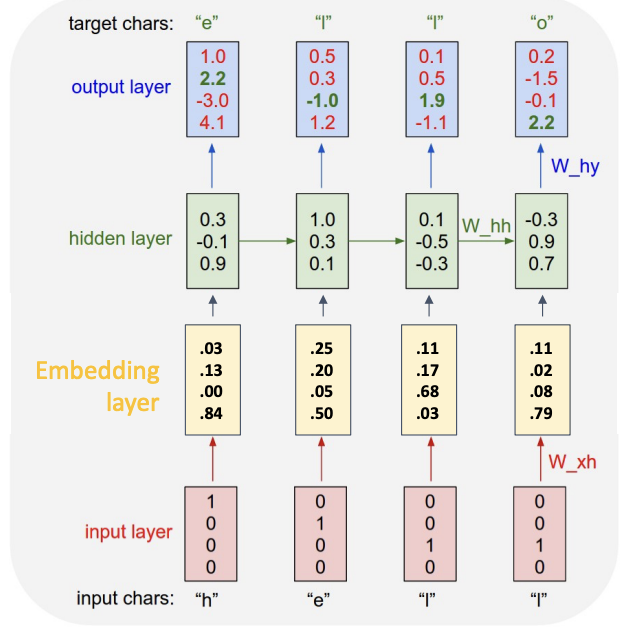
example: Language Modeling
固定的vocabulary,每个字母使用one-hot编码,

At test-time, generate new text: sample characters one at a time, feed back to model
第一步的输出作为下一步的输入
带有one-hot编码的矩阵乘法仅仅提取了权重矩阵的一列,通常将这一步提取出来作为单独的embedding layer
3 Backpropagation Through Time¶
在处理长序列时,所有输出汇聚到一个总的损失函数。
在forward pass的过程中给你,网络需要按时间顺序处理整个输入序列,从第一个时间步一直到最后一个。在这个过程中,计算并存储每个时间步的输入、隐藏状态和输出。最终,根据所有时间步的输出和真实标签计算出总的损失。
Bakcward pass: 计算出总损失后,算法需要反向追溯整个计算路径,从最后一个时间步一直回到第一个,以便计算出每个参数的梯度(gradient)。梯度是用来更新网络权重、从而“学习”的关键。
为了计算梯度,反向传播需要利用前向传播过程中产生的所有中间值(主要是每个时间步的激活值,序列越长,需要存储的中间值就越多,对内存的占用就呈线性增长。当序列长度达到一定程度时,内存就会被耗尽,导致程序崩溃或无法运行,这使得在有限的硬件资源上训练长序列模型变得不切实际
解决方案:Truncated Backpropagation Through Time
不再对整个序列进行一次性的反向传播,而是将长序列切分成若干个较短的子序列,只在每个较短的子序列内部进行。例如,处理完20个时间步后,就进行一次反向传播来计算和更新梯度,但反向传播的路径只回溯这20步,而不是回溯到序列的起点
image captioning: 我们先把图片喂给 CNN, 再把 CNN 提取出的特征喂给 RNN, 让它一个词一个词描述图像, 一般在 RNN 中有一个 start token 开始, 一个 end token 结尾(如果网络预测到了 end token 就立即停止输出)
4 Vanilla RNN Gradient Flow¶
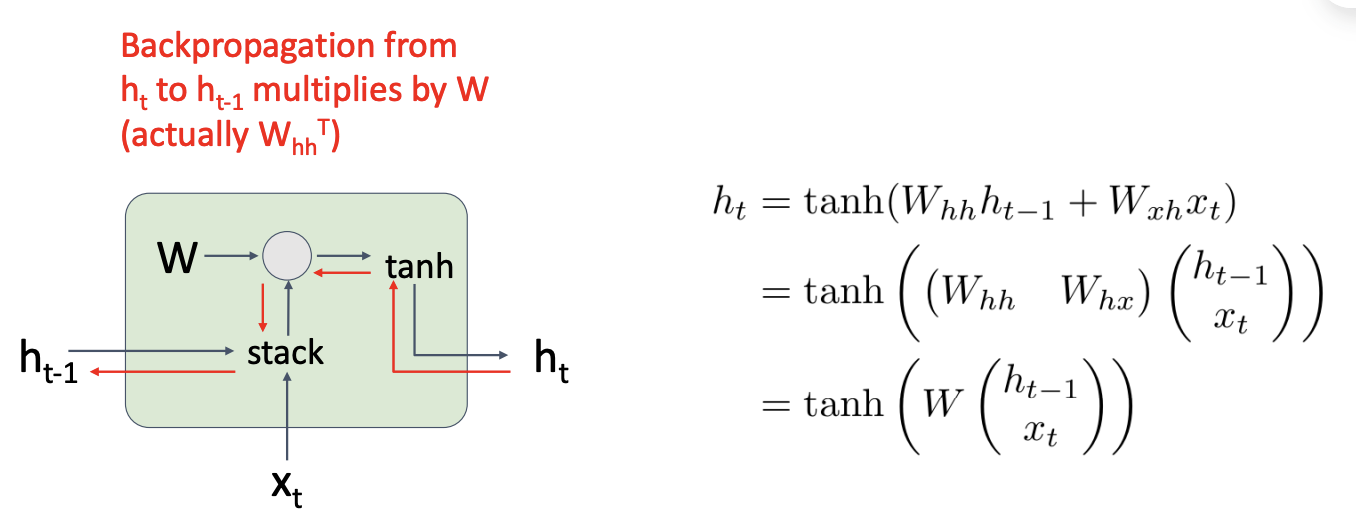
当多个 RNN 单元连接时, 我们会重复乘以同样的权重矩阵 W, 要么会梯度爆炸, 要么会梯度消失
梯度爆炸时, 我们可以做梯度裁剪(gradient clipping), 设置一个梯度上限, 大于上限就乘以一个小系数
但是梯度消失怎么办呢?下面介绍一种新的 RNN 架构: 长短期记忆(Long Short Term Memory)(LSTM)
 保留两个不同的隐藏状态
保留两个不同的隐藏状态
- i: Input gate, 是否写
- f: Forget gate, 是否消除单元
- o: Output fate, 表达单元的程度
- g: Gate gate, 写入单元的程度


反向传播时不会经过权重 \(W\), 只会乘以遗忘\(f\)的系数, 没有非线性也没有矩阵乘法, 一般我们用\(h_t\)做预测, 更像是一种单元的私有变量
目前我们讨论的都是单层 RNN, 通过在隐藏序列上再应用一个 RNN, 我们可以得到一个二层 RNN, 一层处理原始数据得到隐藏序列, 一层处理隐藏序列得到结果, 同理你可以构造多层 RNN