Training Neural Networks 1¶
1 Overview¶
- One time setup: 激活函数,数据预处理,权重初始化, 正则化
- training dynamics:设置学习率,大批次训练,超参数优化
- After training
2 Activation Functions¶

2.1 Sigmoid¶
将输出限制在0和1之间,类比神经元打开或者关闭
但是有效地杀死了梯度,使学习速度非常慢
输出都是正的,不是以0为中心
下一层的输入都会是正的,所以局部梯度一直为正,梯度的正负只由上游决定,都是正的或者负的
指数函数计算开销很大,不过对GPU影响不大
2.2 Tanh¶
sigmoid的一个缩放和移动
zero centered
饱和时梯度仍然接近0
2.3 ReLU¶
不会饱和,计算高效,相较于前两个函数收敛的很快
但是所有的输入都是非负的
输入非常小时,最后的梯度为0,无法进行学习
Dead ReLU,解决方法 Leakly ReLU, \(f(x) = max(0.01x,x)\)
2.4 PReLU¶
\(\alpha\),也进行梯度下降
2.5 ELU¶
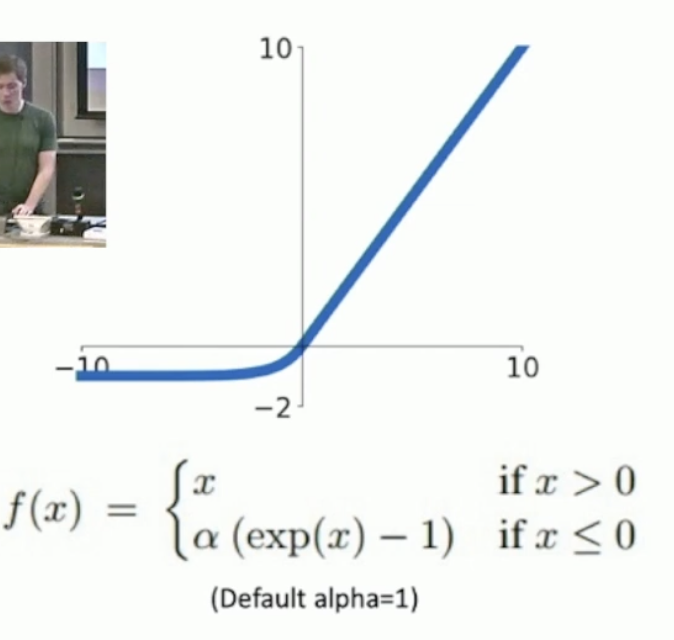
汇集了ReLU 的所有优势
-
更接近于零均值的输出
-
与Leaky ReLU相比,负饱和区间增加了一些对噪声的鲁棒性
2.6 SELU¶

但是激活函数对准确率的影响并没有太大
3 Data Preprocessing¶
- original data
- zero-centered data:
X -= np.mean(X, axis = 0) - normalized data:
X /= np.std(X, axis = 0) - PCA
- Whitening
4 Weight Initialization¶
Xavier Initialization:std = 1/sqrt(Din) W的

使输入输出的方差相同
Kaiming/MSRA Initialization
ReLU correction : std = sqrt(2/Din)
ReLU之后是不对称的

4.1 Residual Networks¶
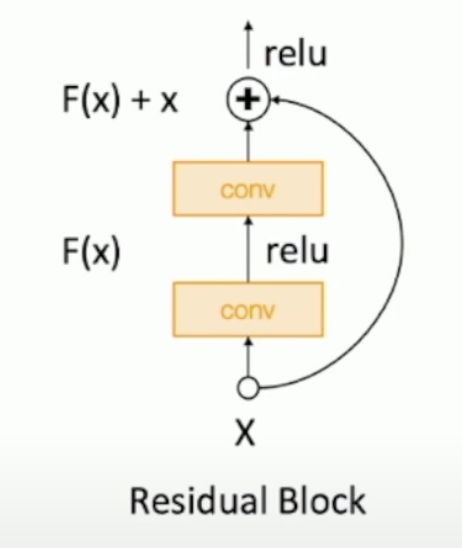
如果一开始使用msra方法初始化权重,\(Var(F(x))=Var(x)\),但是\(Var(F(x)+x)>Var(x)\)
Solution: 第一个卷积层使用MSRA初始化,第二个卷积层初始化为0
5 Regularization¶
常规方法:

5.1 Dropout¶
随机丢弃一些神经元(设置为0)
组织了网络的冗余表达,防止对特质的适应
Dropout是在训练一个共享参数的大型集成模型,每一个二进制掩码就是一个模型
测试时: 根据之前的随机值取平均

测试时使用所有的神经元
Inverted Dropout 通过一个巧妙的“倒置”操作,将尺度缩放的步骤从预测阶段提前到了训练阶
dropout主要应用于全相连层
6 Data Augmentation¶
- 翻转
- 随机大小/剪裁
