1 Computer organization¶

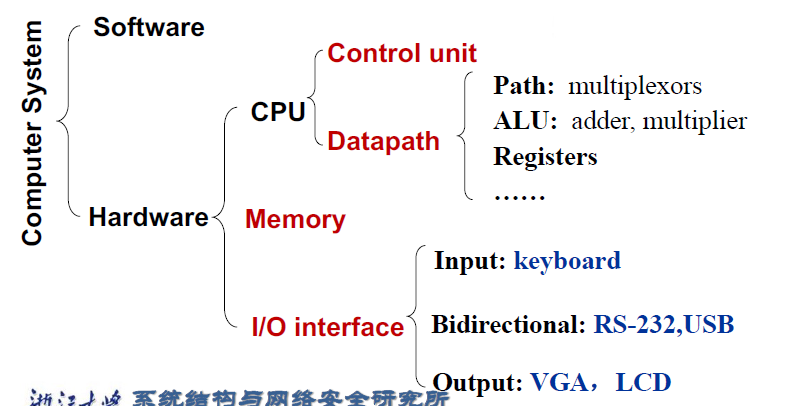
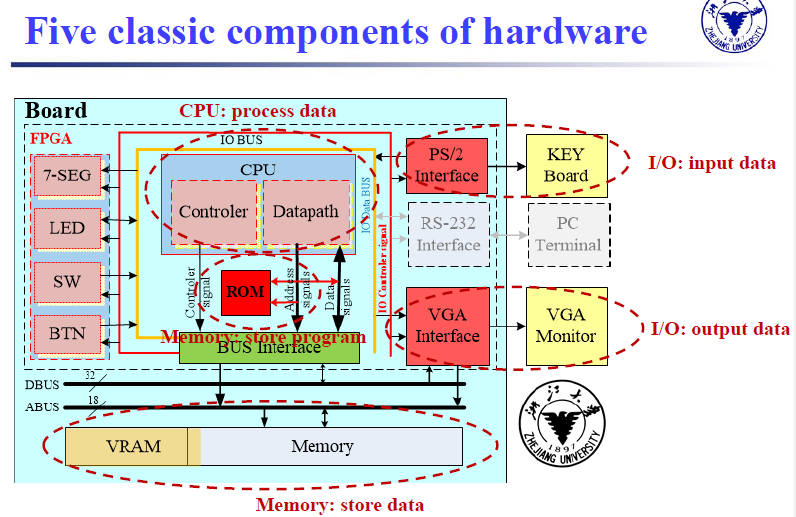
1.1 Software categorization¶

operating system
compiler
fireware（驱动）

2 图灵测试/图灵完备¶

2.1 图灵测试¶

图灵测试（Turing Test）是由英国数学家和计算机科学家艾伦·图灵（Alan Turing）在1950年提出的一种测试，用于判断机器是否具有智能。图灵测试的基本思想是，如果一台机器能够在对话中表现得与人类无异，那么这台机器就可以被认为具有智能。

2.1.1 图灵测试的基本过程：¶

参与者：测试中有三方参与者：一个人类评审员（C），一个人类参与者（A），和一个机器参与者（B）。
隔离：评审员与参与者之间通过文本进行交流，评审员无法看到或听到参与者，只能通过打字进行交流。
对话：评审员与人类参与者和机器参与者分别进行对话，评审员的任务是判断哪个是人类，哪个是机器。
判断：如果评审员无法可靠地区分人类和机器，或者机器能够成功地欺骗评审员，使其认为机器是人类，那么机器就通过了图灵测试。

图灵测试的核心在于机器能否在自然语言对话中表现出与人类无异的智能，而不是机器的内部工作原理或其实现方式。

2.2 图灵完备¶

图灵完备（Turing Completeness）是计算理论中的一个概念，用于描述一个系统（通常是编程语言或计算模型）的计算能力。一个系统被称为图灵完备的，如果它能够模拟图灵机的计算能力，即能够执行任何图灵机可以执行的计算。

2.2.1 图灵完备的基本条件：¶

条件分支：系统必须能够执行条件分支（如if-else语句），以便根据不同的条件执行不同的操作。
循环：系统必须能够执行循环（如for、while语句），以便重复执行某些操作。
存储和操作数据：系统必须能够存储和操作数据，包括读写变量和数据结构。

2.2.2 图灵完备的意义：¶

通用性：图灵完备意味着该系统具有通用计算能力，可以解决任何可计算的问题，只要有足够的时间和资源。
编程语言：大多数现代编程语言（如C、Java、Python等）都是图灵完备的，因为它们具备条件分支、循环和数据操作的能力。
计算模型：图灵完备的计算模型包括图灵机、λ演算（Lambda Calculus）等，这些模型为计算理论提供了基础。

2.3 From a High-Level Language to the Language of Hardware¶

Machine language 由二进制数表示指令
Assembly language the assembler translates them into machine instruction
High-level programming language the compiler translates into assembly language

2.4 Integrated circuits/集成电路¶

Both processor and memory are made of integrated circuits

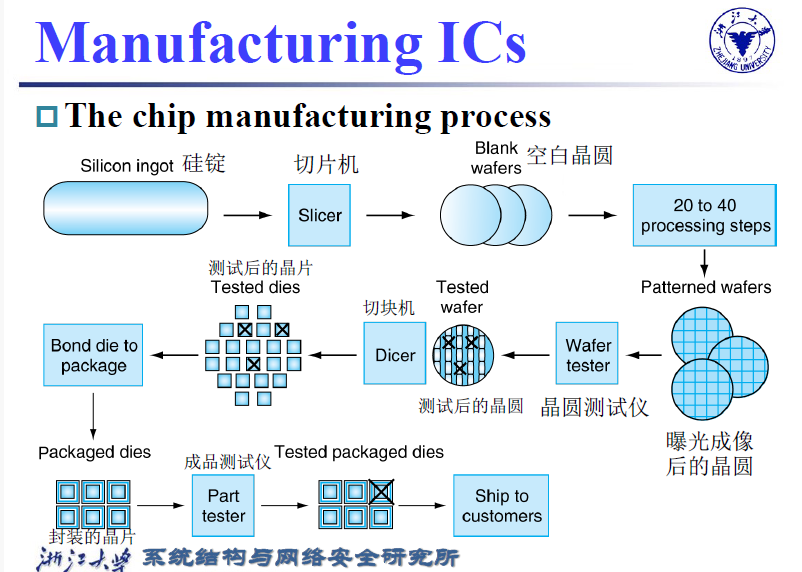
3 Computer design: performance and idea¶

Response time/ execution time
throughput(total work done per unit time)

3.1 Relative Performance¶

3.2 Measuring Execution Time¶

Elapse time total response time: processing, I/O, OS overhead, idle time
CPU time CPU时间（CPU Time）是指程序在CPU上实际执行的时间。它只计算CPU在处理程序指令时所花费的时间，不包括程序等待I/O操作或其他进程执行的时间。
clock period: duration of a clock cycle
clock frequency(rate): cycles per second

3.2.1 CPU Time¶

\[CPU~Time=\frac {CPU~Clock ~Cycles}{Clock ~Rate}$$ - Performance improved by - Reducing number of clock cycles - Increasing clock rate - Hardware designer must often trade off clock rate against cycle count $${Clock~Cycles=Instruction Count\times {Cycles ~per~ Instruction}} \newline $$ $${CPU ~Time}= Instuctinon ~Count\times \frac{CPI} {Clock Rate} $$ 如果不同的指令集消耗了不同的时钟周期，分开计算 - Weighted average CPI则取平均 $$CPI=\frac {Clock~cycles}{Instruction Count}$$ **Performance Summary** $$CPU~Time=\frac {Instructions}{Program}\times\frac{Clock Cycles}{Instruction}\times\frac{Seconds}{Clock cycle}\]

performance depends on: - Algorithm: affects IC, possibly CPI - Programming language: affects IC, CPI - Compiler : affects IC， CPI - Instruction set architecture: affects IC,CPI, $T_c$

3.3 Power Trends¶

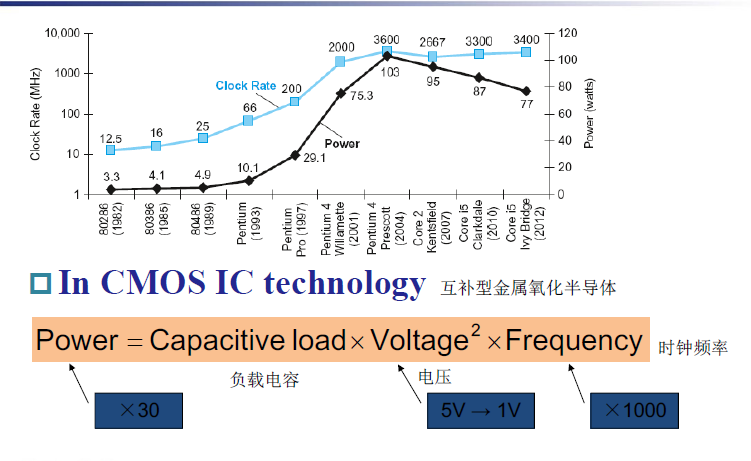
4 Multiprocessors¶

More than one processor per chip - requires explicitly parallel programming - hard to do: - programming for performance - load balancing负载平衡 - optimizing communication and synchronization通信和同步

4.1 Amdahl's Law¶

通过优化系统的单个部分而获得的整体性能提升受到改进部分实际使用的时间的限制有一部分的程序只能通过串行进行访问 5.2 MIPS

5 Eight Great Ideas¶

Design for Moore's Law integrated circuit resources double every 18–24 months
Use Abstraction to Simplify Design use abstraction to characterize the design at different levels of representation; 抽象，封装
Make the Common Case Fast (加速大概率事件)
performance via parallelism(通过并行提高性能)
performance via pipelining(通过流水线提高性能)
performance via prediction(通过预测提高性能)
hierarchy of memories(存储器层次)
dependability via redundancy(通过冗余提高可靠性)

Chapter 3: Arithmetic for computer¶

1 Numbers¶

sign-magnitude 原码
1's complement code 反码
2's complement code 补码
biased notation 移码（在补码的基础上，符号位取反）

1.1 Number Types¶

2 Overflow¶

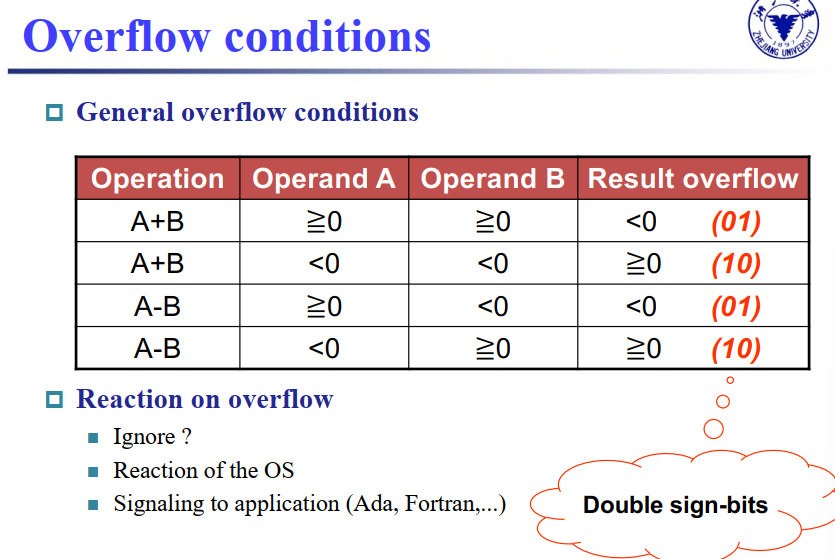slt: set on less than

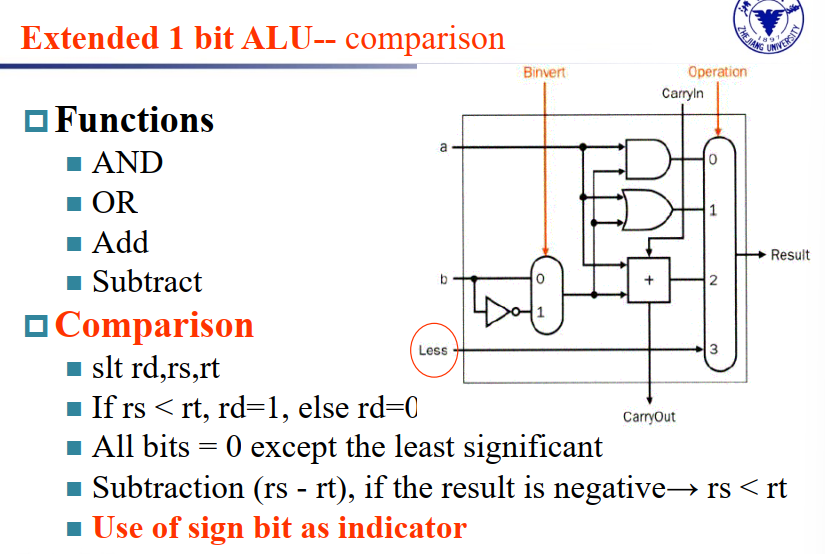
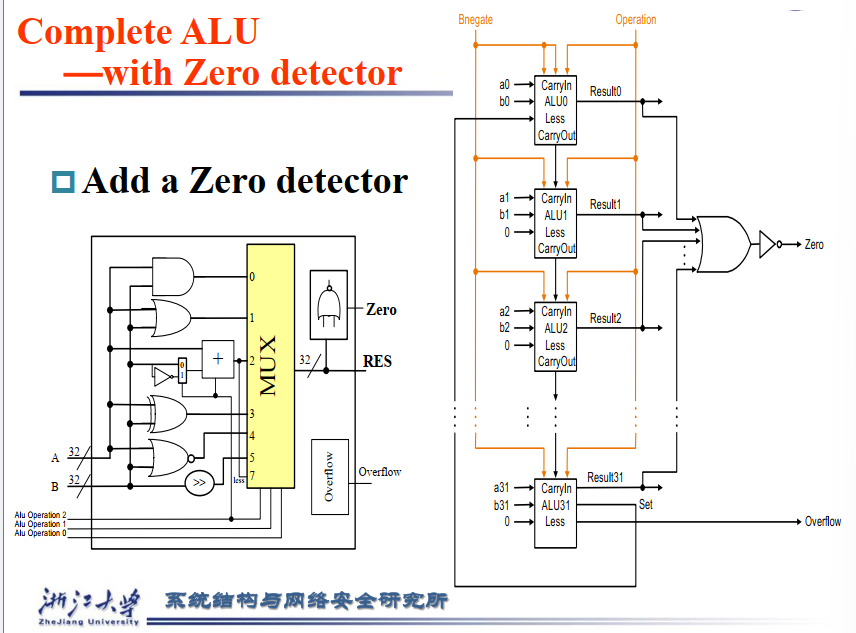
3 Complete ALU¶

Input
- A,B
Control lines
- Binvert
- Operation
- Carry in
Output
- Result
- overflow
Slow, but simple
- Inputs parallel
- Carry is cascaded
  - Ripple carry adder

3.1 with Zero detector¶

4 Fast adders¶

4.1 Carry look-ahead adder(CLA)¶

提前计算会不会产生进位 - $A_i,B_i$都是1 - $A_i,B_i$其中一个是1，且有进位 two signal conditions are called - generate$G_i$ - propagate $P_i$ 推导公式 $$\begin{align} &P_i=A_i\oplus B_i\ &G_i=A_iB_i\ &S_i=P_i\oplus C_i\ &C_{i+1}=G_i+P_iC_i \end{align} $$ 四位全加器 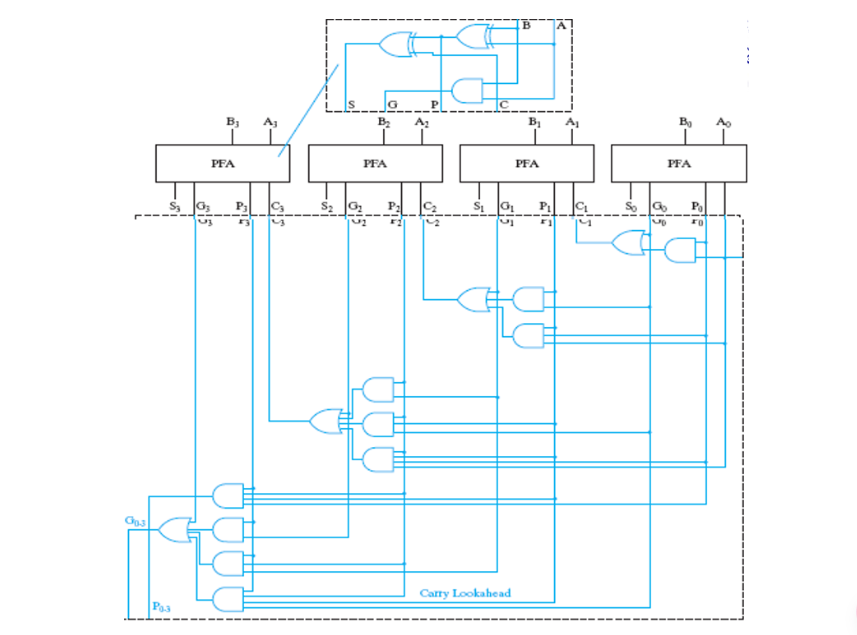PFA（Partial Fully Adder, 用于上述四个变量的计算对于位数更多的加法器，我们利用这样构成的4-比他CLA通过类似的方式串起来

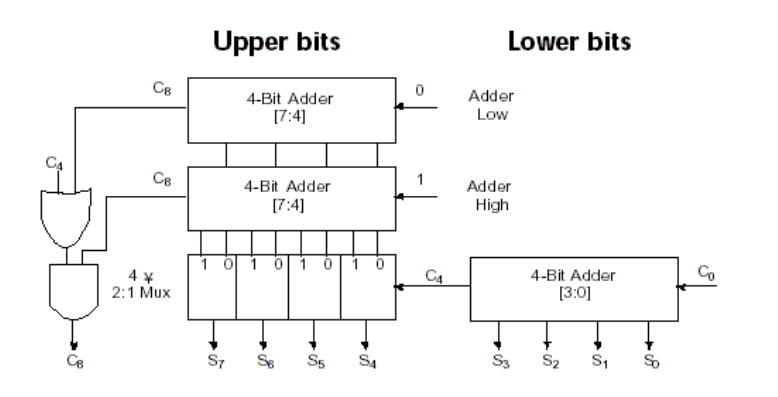
4.2 Carry select adder(CSA)¶

5 Multiplication¶

移位$\rightarrow$相乘$\rightarrow$相加

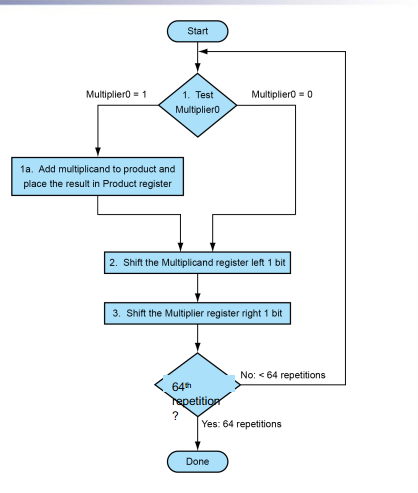
5.1 V1¶

需要64次迭代
- Addition
- Shift
- Comparison

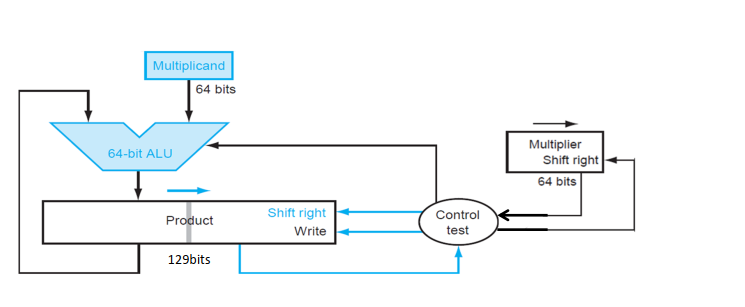
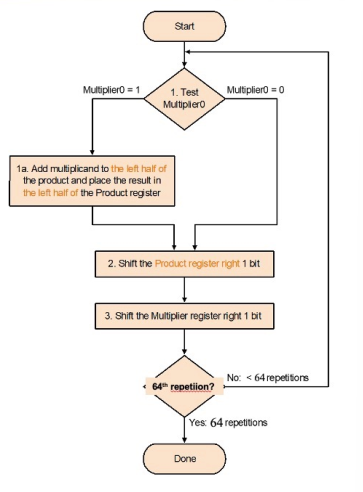
5.2 V2¶

Don't shift the multiplicand
Instead, shift the product
Shift the multiplier 129位的product 寄存器是为了保留进位

5.3 V3¶

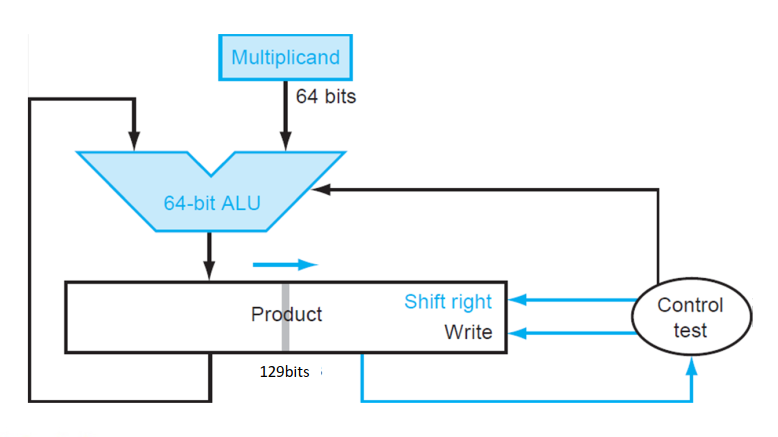- 积寄存器设为0 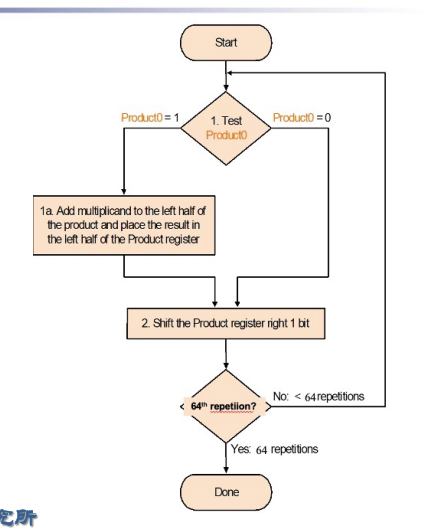就是把原来的product和multiplier首尾相连放在同一个寄存器里面，在每一次乘积之后都一起右移

6 Signed multiplication(有符号数的乘积)¶

basic approach: - 存储符号位 - 判断同号还是异号 - 数值部分相乘 - 再加上符号位

6.1 Booth's Algorithm¶

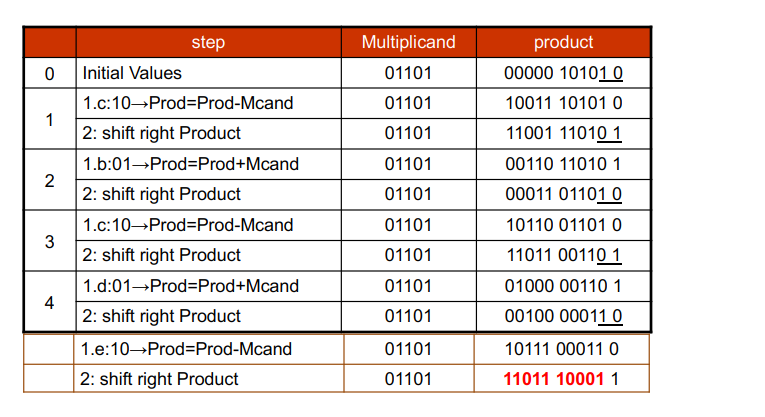
优化符号数乘法 idea: Booth's Algorithm 的主要思想在于，减少乘数中“1”的数量。具体来说，在我们原先的乘法策略中，每当乘数中有一位 1 时，都会需要一个加法（将位移后的被乘数累加到结果中）。但是，如果乘数中有较长的一串 1 时，我们可以将它转化为一个大数字减一个小数，如：00111100 = 01000000 - 00000100，此时 4 个 1 变为 2 个 1，我们就可以减少做加法的次数

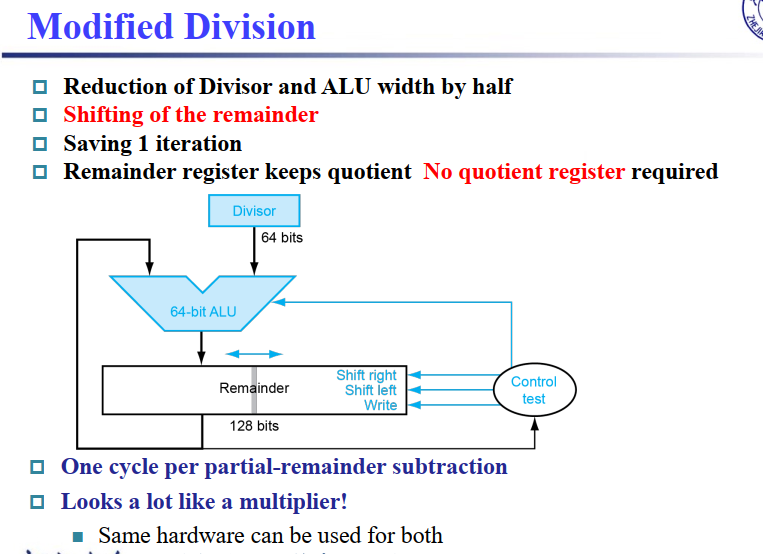
6.2 Faster Multiplication¶

6.3 RISC-V Multiplication¶

Four multiply instructions: - mul: 给出乘积的低64位 - mulh：高64位 - mulhu：无符号，高64位 - mulhsu：一有一无

7 Division除法¶

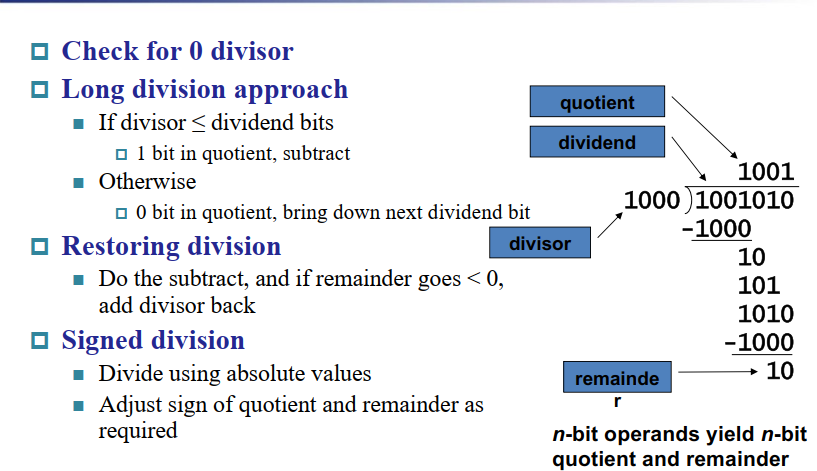
7.1 Division V1¶

首先，除数在除数寄存器的左半部分，被除数在结果的右半部分每一步之后右移一位 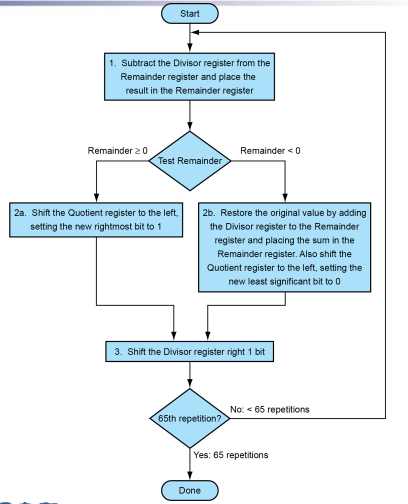为什么被除数要被放在右半部分？

7.2 Division V2¶

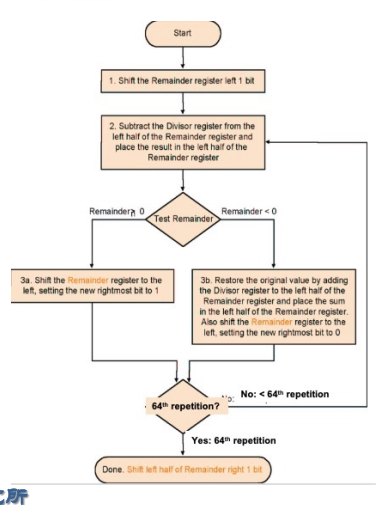remainders左移，商补充在右边

7.3 Signed division¶

若同号则quotient为正，异号则为负，若dividend为正，则remainder为正，否则remainder为负 Faster Division

7.4 RISC-V Division¶

instructions: - div ,rem: 有符号，remainder - divu,remu: 无符号，remainder

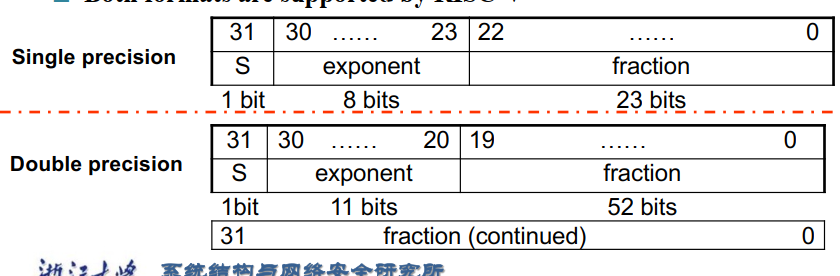
7.5 Floating point numbers¶

我们将小数点左边只有 1 位数字的表示数的方法称为 科学记数法, scientific notation，而如果小数点左边的数字不是 0，我们称这个数的表示是一个 规格化数, normalized number。科学记数法能用来表示十进制数，当然也能用来表示二进制数。

我们将浮点数表示为$(-1)^S\times F\times 2^E$的形式 0用特殊的方式保存 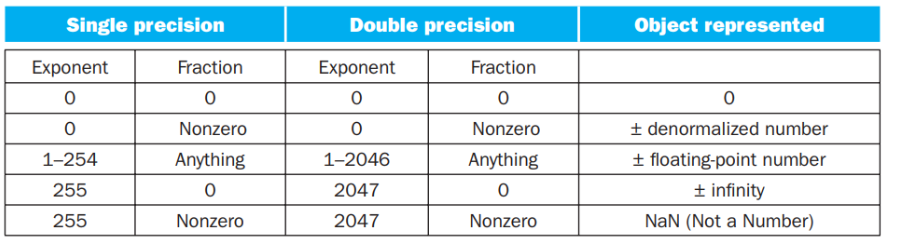在上表中： - 第一条表示0 - 第二条表示非规格化数，主要是为了用来表示一些很小的数，它的取值为$(-1)^S\cdot(0+fraction)\cdot 2^{-bias}$ - 第三条表示正常的浮点数 - 第四条表示无穷大或者无穷小，出现在exponent overflow或者浮点数运算中非0除以0的情况 - 第五条表示非数，出现在$\frac 00,\frac{inf}{inf},inf-inf,inf*0$的情况范围精度

7.5.1 浮点加法¶

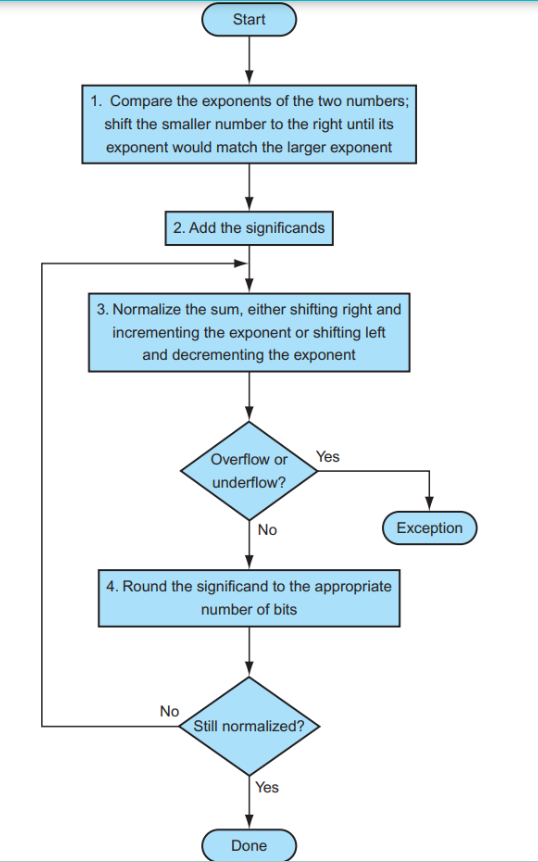
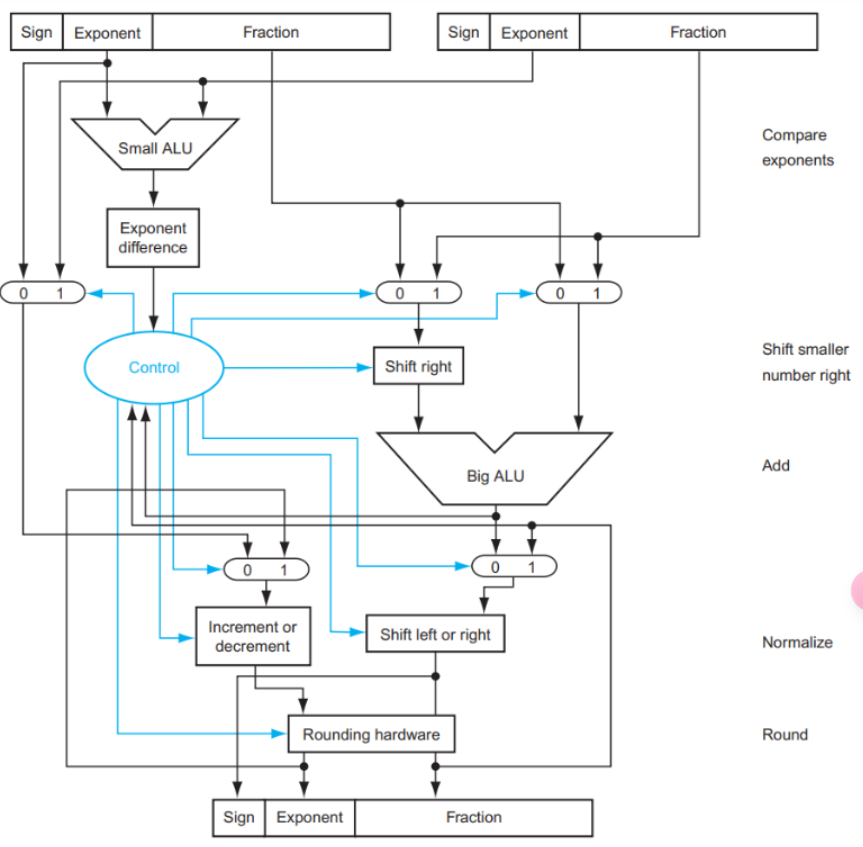
浮点数的加减法分为以下几步： - Alignment:指数对齐，将小指数对齐到大指数 - Addiction Fraction：部分相加减 - Normalization: 将结果规格化，并检查是否出席那overflow或者underflow，如果出现则出发Exception - Rounding: 将Fraction部分舍入到正确的位数；舍入结果可能还需要规格化，此时回到上一个步骤继续运行

7.5.2 浮点乘法¶

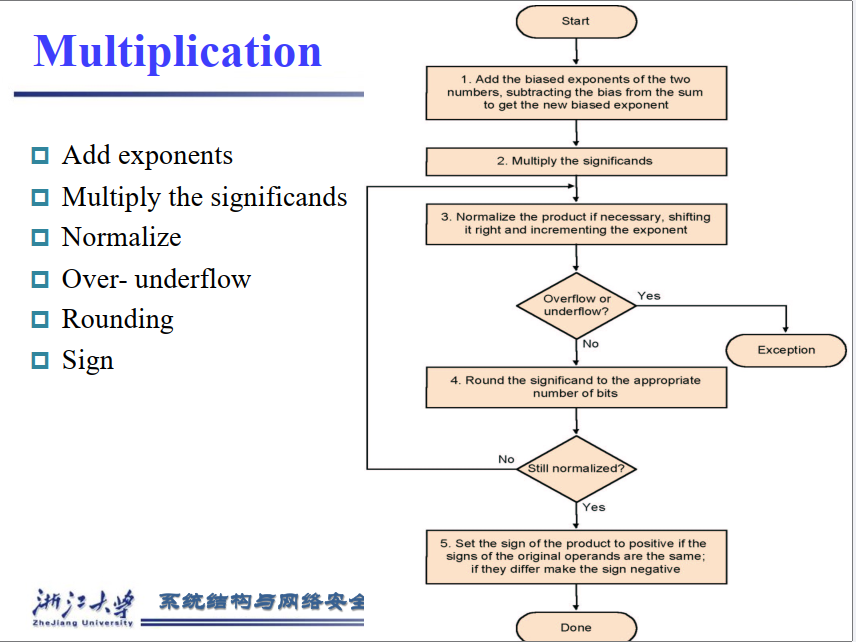
分别处理符号位，exponent，fraction - 将两个Exponent 相加并减去一个bias,因为bias 加了两次 - 将两个(1+Fraction)想乘，并将其规格哈，此时同样要考虑overflow和underflow，然后舍入，如果还需要规格化则重复执行 - 根据两个操作数的符号决定结果的符号

7.6 精确算术¶

Round modes - guard/round/sticky 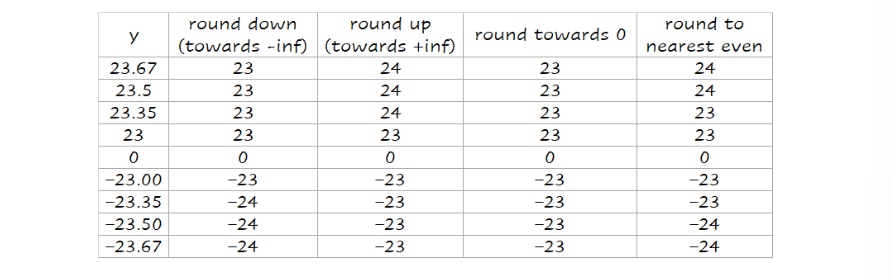Round to nearest even 只对0.5有效，别的都和四舍五入一样一般的浮点数后面还会有2bits，分别称为guard和round，其主要目的是让计算结果的舍入更加精确

事实上加法只需要用到guard，但是对于乘法，如果存在前导0，需要将结果作业，这时候round bit 就成了有效位

另外还有一个位叫 sticky bit，其定义是：只要 round 右边出现过非零位，就将 sticky 置 1，这一点可以用在加法的右移中，可以记住是否有 1 被移出，从而能够实现 "round to nearest even"。